Ավետ Սարդարյան

Բազմանկյուն կոչվում է պարզ փակ բեկյալից և նրանով սահմանափակված տիրույթից բաղկացած պատկերը:

Բեկյալի հանգույցները կոչվում են բազմանկյան գագաթներ, իսկ օղերը՝ կողմեր:

Երկու ոչ հարևան գագաթները (որոնք չեն գտնվում նույն կողմի վրա) միացնող հատվածը կոչվում է բազմանկյան անկյունագիծ:

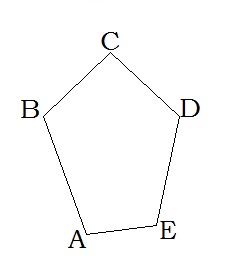
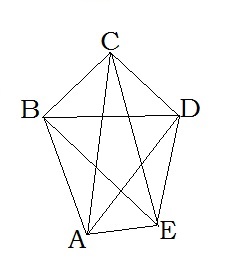
A, B, C, D, E՝ գագաթներ,

AB, BC, CD, DE, AE՝ կողմեր,

AC, AD, BE, BD, CE՝ անկյունագծեր: 

Յուրաքանչյուր քազմանկյուն հարթությունը բաժանում է երկու մասի, որոնցից մեկը կոչվում է բազմանկյան ներքին տիրույթ, իսկ երկրորդը՝ արտաքին տիրույթ:

Ուռուցիկ բազմանկյուն․

Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող ուղղի մի կողմում։

ABCDE հնգանկյունը ուռուցիկ է:  

Ուռուցիկ n-անկյան անկյունների գումարը 180°⋅(n−2) է:

Օրինակ՝

Հաշվենք տասնմեկանկյան անկյունների գումարը:

Կիրառելով բանաձևը, ստանում ենք՝
180°⋅(n−2)=180°⋅(11−2)=180°⋅9=1620°

Կանոնավոր բազմանկյուններ․

Այն ուռուցիկ բազմանկյունը, որի բոլոր կողմերը և անկյունները հավասար են, կոչվում է կանոնավոր բազմանկյուն:

Կանոնավոր եռանկյունը հավասարակողմ եռանկյունն է:

Կանոնավոր քառանկյունը քառակուսին է:

Քառանկյուններ․

Բազմանկյունը կոչվում է քառանկյուն, եթե այն ունի 4 կողմ:

Քառանկյունն ունի 4 կողմ, 4 գագաթ, 4 անկյուն, 2 անկյունագիծ: Քառանկյան ոչ կից կողմերը կոչվում են հանդիպակաց:

Ուռուցիկ բազմանկյան անկյունների գումարի բանաձևի մեջ n-ի փոխարեն 4 տեղադրելով, ստանում ենք հետևյալ պնդումը:

Ուռուցիկ քառանկյան անկյունների գումարը հավասար է 360°-ի:

Առաջադրանքներ․

1)Քառանկյան կողմերը հարաբերում են, ինչպես 3:4:5:7: Գտե՛ք քառանկյան կողմերը, եթե պարագիծը 380սմ է։

3x+4x+5x+7x=380
19x=380
x=20

3x=60 սմ
4x=80 սմ
5x=100 սմ
7x=140 սմ

Կողմեր, 60 սմ, 80 սմ, 100 սմ, 140 սմ:

2)ABCD ուռուցիկ քառանկյունում <A = 20o , <B = 90o, իսկ C անկյունը 30օ-ով մեծ է D անկյունից։ Գտե՛ք <C-ն և <D-ն։

360-90-20=250

250:2=125

∠d=125-30=95

∠c=125+30=155

3)Քանի՞ կողմ ունի ուռուցիկ բազմանկյունը, եթե նրա անկյունների գումարը 540o է։

540:180=3

4)Գտե’ք ուռուցիկ քառանկյան անկյունները, եթե դրանցից մեկը մյուսներից մեծ է համապատասխանաբար 10o-ով, 20o-ով , 30o-ով։

130, 120, 110, 140.

5)Գտե’ք ուռուցիկ հնգանկյան անկյունները, եթե դրանք համեմատական են 5, 6, 4, 6, 6 թվերին։

Ուռուցիկ հնգանկյան անկյունները լինում են՝

Պատասխան 90°, 108°, 72°, 108°, 108°.

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք ABCD քառանկյան պարագիծը, եթե AB=12սմ, BC=21սմ, CD=14սմ, AD=15սմ։

12+21+14+15=62

2)Հնգանկյան կողմերը հարաբերում են, ինչպես 2:3:5:7:8: Գտե՛ք հնգանկյան պարագիծը, եթե դրա ամենամեծ կողմը 16սմ է։

16:8=2

2×2=4

2×3=6

2×5=10

2×7=14

16+14+10+6+4=50

3)Գտե՛ք ուռուցիկ քառանկյան անկյունները, եթե դրանք համեմատական են 1, 2, 4, 5 թվերին։

Անկյունները լինում են հետևյալը՝

x = 30

1. 30
2. 60
3. 120
4. 150

Պատասխան 30°, 60°, 120°, 150°.